• हम तारों की दूरी कैसे ज्ञात कर लेते है ?
• हम कैसे बता पाते है की उस तारे की दूरी उतनी है इस तारे की दूरी इतनी है ?

यह ऐसे सवाल है जो विज्ञान विश्व पृष्ठ पर सबसे ज्यादा लोगो ने सबसे ज्यादा बार पूछा है। ब्रह्माण्ड में स्थित तारों, ग्रहों या आकाशगंगाओं की दूरी को मापना कोई आसान काम नही होता क्योंकि पृथ्वी से इनकी दूरी आमतौर पर बहुत ज्यादा होती है। खगोलविज्ञानी ब्रह्माण्डीय दूरी को मापने के लिए कई विभिन्न तरीकों का उपयोग करते है। खगोलीय दूरी मापने में उपयोग होनेवाली सभी विधियां विज्ञान और गणित के अद्भुत संयोजन का उदाहरण है।

• राडार मापन(Radar Measurement)
• लंबन विधि(Parallax method)
• सीफीड मापन(Cepheids Measurement)
• सुपरनोवा मापन(la Supernova Measurement)
• लाल विचलन और हबल सिद्धान्त द्वारा मापन(Redshift and Hubble’s Law Measurement)

राडार मापन(Radar Measurement):

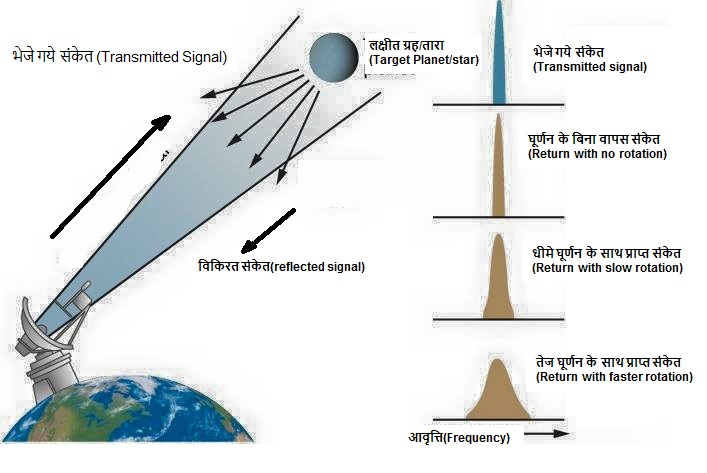
:दूरी मापने का यह भी एक आधुनिक तरीका है। यह विधि इस तथ्य पर आधारित है की प्रकाश(रेडियो तरंग, माइक्रोवेव, दृश्य प्रकाश, X-किरण) 300000 km/s की रफ़्तार से यात्रा करता है। यह तकनीक सबसे सटीक मानी जाती है लेकिन इस विधि की भी अपनी सीमाएं है। खगोलविज्ञानी इस विधि से सौरमंडल तक कि दूरी तो निर्धारित कर सकते है लेकिन इससे अधिक दूरी के लिए यह विधि उपयोगी नही है। वैज्ञानिकों ने सौरमंडल में स्थित ग्रहों की दूरी निर्धारण के लिए इस तकनीक का उपयोग कई बार किया है खासकर पृथ्वी से चंद्रमा की दूरी मापने के लिए यह सबसे नियमित तरीका है।

इस विधि में पृथ्वी से संचारित संकेत(Transmitted signal) उस पिंड/ग्रह पर भेजे जाते है। संकेत उस ग्रह से टकराकर वापस लौटने पर पृथ्वी के संचारित केंद्रों द्वारा पकड़ लिए जाते है। वैज्ञानिक संचारित संकेतो के जाने और लौटने में लगने वाले समय को दर्ज कर लेते है इससे उस ग्रह की दूरी का पता लगा लिया जाता है।

D(Distance) = V(Velocity) × T(Time)

लंबन विधि(Parallax method):

खगोलविज्ञानी अंतरिक्ष में स्थित किसी तारे की दूरी को पता करने के लिए सामान्यतः एक खास विधि का उपयोग करते है जिसे लंबन/तारकीय लंबन(Stellar Parallax) कहते है। दो विभिन्न बिंदुओं से किसी वस्तु की ओर देखने पर जो कोणीय विचलन(angular shift) प्रतीत होता है, उसे लंबन कहते हैं और इन बिंदुओं को मिलानेवाली आधार रेखा उस दूरस्थ वस्तु पर जो कोण बनाती है, उससे लंबन का निरूपण होता है। सरल शब्दों में लंबन दो अलग-अलग स्थानों से देखा गया किसी तारे की स्पष्ट स्थिति में अंतर ही है जो उसके बैकग्राउंड में स्थित वस्तुओं के कारण प्रतीत होता है। आधार रेखा जितनी ही बड़ी होगी(अर्थात्‌ प्रेक्षण के बिंदु जितने ही दूर होंगे) वस्तु पर कोण उतना ही बड़ा होगा और परिणाम में सटीकता/यथार्थता की संभावना भी उतनी ही ज्यादा होगी।

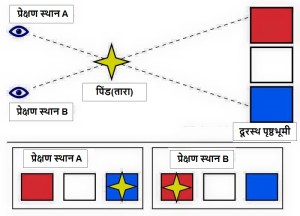
अब सवाल है लंबन विधि द्वारा बड़ी दूरियों जैसे ग्रह अथवा तारे की दूरी का मापन हम कैसे करते है ? सबसे सरल तरीका है गणितीय विधि।

किसी दूरस्थ तारे/ग्रह S की दूरी D ज्ञात करने के लिए, हम इसको पृथ्वी पर स्थित दो वेधशालाओं से भी प्रेक्षण कर सकते है लेकिन जैसा हमने ऊपर बताया की प्रेक्षण के बिंदु जितने ही ज्यादा दूर होंगे परिणाम की सटीकता उतना ही बेहतर होगी। इसलिए खगोलविज्ञानी पृथ्वी के परिक्रमण व्यास को अपनी प्रेक्षण बिंदु बनाते है इसके लिए बस खगोलविदों को 6 महीने के अंतराल पर प्रेक्षण करना पड़ता है।

मान लीजिए प्रेक्षण बिंदु A तथा B है।

A एवं B के बीच की दूरी AB = b

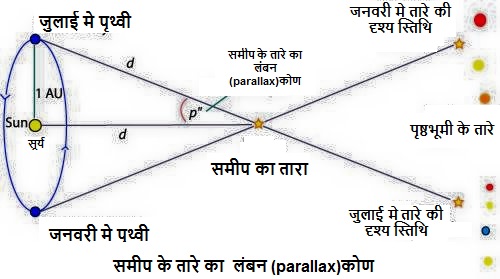
इन दो स्थितियों से तारे की प्रेक्षण दिशाओं AS तथा BS के बीच का कोण θ = ∠ ASB माप लिया जाता है। यह कोण लम्बन कोण या लम्बनिक कोण(parallax angle) कहलाता है।
तारे की पृथ्वी से दूरी D बहुत अधिक है अतः

b << D

इसलिए कोण θ बहुत ही छोटा है। अतः हम S को वृत्त का केंद्र, AS = D को त्रिज्या तथा AB = b चाप मान सकते हैं।

∵ त्रिज्या AS = BS,
∴ चाप AB = b
∵ कोण θ = चाप/त्रिज्या = AB/AS
θ = b/D
अतः तारे की दूरी
D = b/θ

इस सूत्र में मान रख कर लम्बन-विधि से ग्रह अथवा तारे की पृथ्वी से दूरी ज्ञात कर सकते हैं। यहाँ पर पृथ्वी के परिक्रमण व्यास को अपनी प्रेक्षण बिंदु बनाया गया है इसलिए वह दूरी 2AU(खगोलीय इकाई: Astronomical unit) है।

∴ तारे की दूरी D(Parsec) = 1/p(arcseconds).

दूरस्थ तारों का लंबन कोण बहुत ही छोटा होता है उसका मापन अर्कसेकंड(arcseconds) में किया जाता है। चूंकि तारों की दूरी भी बहुत अधिक होती है इसलिए उसका मापन भी पारसेक(Parsec) में किया जाता है। यदि किसी तारे का लंबन कोण 0.723 अर्कसेकंड है तो उस तारे की दूरी होगी
D = 1/0.723 = 1.38 पारसेक।

लंबन विधि तारो की दूरी ज्ञात करने के लिए एक अच्छी विधि है लेकिन इस विधि की भी अपनी सीमाएं है। नजदीकी तारों की दूरी ज्ञात करने में यह विधि बेहद कारगर है लेकिन बहुत ज्यादा दूरी पर स्थित तारों के लिए यह विधि उपयोगी नही है। यदि ज्ञात लंबन कोण 0.01 अर्कसेकंड से भी छोटी है तब तारो की दूरी तय करना बड़ा कठिन होता है खासकर तब जब आपका प्रेक्षण बिंदु पृथ्वी पर ही स्थित हो क्योंकि ऐसी स्थितियों में पृथ्वी का वातावरण भी बड़ा प्रभाव डाल देता है। यही वजह है की पृथ्वी पर स्थित टेलिस्कोप के मुकाबले अंतरिक्ष में स्थित टेलिस्कोप तारों की दूरी संबंधित ज्यादा अच्छे परिणाम देते है। अंतरिक्ष में स्थित टेलिस्कोप 0.001 अर्कसेकंड/लंबन कोण पर भी दूरी का सटीक आकलन करने में सक्षम है।
अभी भी आप सोच रहे होंगे की ये तो केवल 100 या 1000 पारसेक दूर स्थित तारों की दूरी ज्ञात करने की विधि है जबकि तारो की ब्रह्मांडीय दूरी तो बहुत ज्यादा है। यहां हम अन्य विधियों की भी चर्चा करेंगे जो बड़ी खगोलीय दूरी मापने में प्रयोग में लायी जाती है।

सीफीड मापन(Cepheids Measurement):

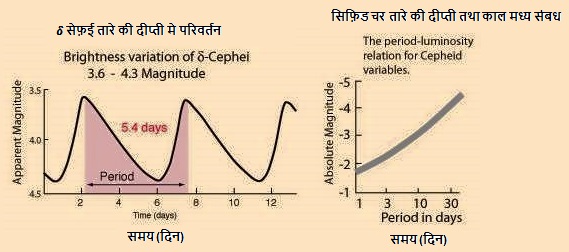
सीफीड मापन(Cepheids Measurement): सीफीड जिसे सीफीड परिवर्तन भी कहा जाता है। कुछ तारों में एक ख़ास गुण होता है वे अपने चमक को एक ख़ास अवधि में बढ़ाते और घटाते रहते है। वर्ष 1908 में, अमेरिकी खगोलविद हेनरिटा स्वान लीविट(Henrietta Swan Leavitt) जब मैग्लेनिक बादल(Magellanic Clouds) का अध्ययन कर रही थी तब उन्होंने एक तारे में इस गुण को देखा। उस तारे की चमक कभी तेज तो कभी मंद हो रही थी, उन्होंने उस तारे के अध्ययन के दौरान पाया की, उस तारे की उज्ज्वलता और मंदता का समय अवधि से बड़ा गहरा संबंध है। 1912 में प्रकाशित अपने अध्ययन में उन्होंने कहा सीफीड तारे एक निश्चित समय अंतराल में अपनी चमक में उतार चढ़ाव प्रदर्शित करते है।

तारों का यह व्यवहार भी वैज्ञानिकों को दूरी मापने के लिए एक खगोलीय मापदंड प्रदान करता है जिससे वैज्ञानिक लाखों प्रकाशवर्ष दूर स्थित तारों की दूरी का आंकलन कर पाते है। सीफीड परिवर्तनशील तारे बेहद चमकीले होते है इन तारों की चमक सूर्य से 500 से 30000 गुणा तक ज्यादा हो सकती है। खगोल वैज्ञानिक सीफीड तारों की उज्ज्वलता और समय अवधि को बड़ी बारीकी से मापते है फिर पूर्ण और स्पष्ट आंकड़ो को दूरी मापांक समीकरण में स्थापित किया जाता है। इस तकनीक से लाखों प्रकाशवर्ष दूर स्थित तारों की दूरी का आंकलन किया जाता है। वैसे दूरी मापांक समीकरण को समझने से पहले आपको निरपेक्ष और सापेक्ष कांतिमान को समझना होगा।

निरपेक्ष कांतिमान/चमक(Absolute Magnitude):

निरपेक्ष कांतिमान/चमक(Absolute Magnitude): निरपेक्ष कांतिमान किसी खगोलीय वस्तु के अपने चमकीलेपन को कहते हैं। मिसाल के लिए अगर किसी तारे के निरपेक्ष कांतिमान की बात हो रही हो तो यह देखा जाता है कि यदि वह तारा ठीक 10 पारसेक की दूरी पर होता तो वह कितना चमकीला लगता। यदि सूर्य हमसे 10 पारसेक की दूरी पर होता तो वह कितना चमकीला हमें दिखता। वैसे सूर्य का मैग्निट्यूड -26.7 है यदि 10 पारसेक दूर सूर्य को भेज दे तो उसका मैग्निट्यूड +4.8 हो जाएगा। सरल शब्दों में आप कह सकते है की सूर्य का निरपेक्ष चमक +4.8 है।

सापेक्ष कांतिमान/चमक(Apparent Magnitude)

सापेक्ष कांतिमान/चमक(Apparent Magnitude): सापेक्ष कांतिमान किसी खगोलीय वस्तु के पृथ्वी पर बैठे प्रेक्षक द्वारा प्रतीत होने वाले चमकीलेपन को कहते हैं। सापेक्ष कान्तिमान को मापने के लिए यह शर्त होती है कि आकाश में कोई बादल, धूल, वगैरा न हो और वह वस्तु साफ़ देखी जा सके। निरपेक्ष कांतिमान और सापेक्ष कांतिमान दोनों को मापने की इकाई मैग्निट्यूड(Magnitude) है।

निरपेक्ष कान्तिमान किसी वस्तु की स्वयं की चमक का माप है और इसमें हमेशा यह देखा जाता है कि 10 पारसेक की मानक दूरी पर वह वस्तु कितनी रौशन लगती है। मिसाल के लिए अगर किसी तारे के निरपेक्ष कांतिमान की बात हो रही हो तो यह देखा जाता है कि यदि देखने वाला उस तारे के ठीक 10 पारसेक की दूरी पर होता और उन दोनों के बीच में कोई खगोलीय धूल वग़ैराह न हो तो वह तारा उसे कितना चमकीला लगता। इस तरह से “निरपेक्ष कांतिमान” और “सापेक्ष कांतिमान” में गहरा अंतर है।
खगोलशास्त्र में खगोलीय कान्तिमान किसी खगोलीय वस्तु की चमक का माप है। इसका अनुमान लगाने के लिए लघुगणक(लॉगरिदम: Algorithm) का इस्तेमाल किया जाता है। मैग्निट्यूड के आंकडे परखते हुए एक ध्यान-योग्य चीज़ यह है के किसी वस्तु का मैग्निट्यूड जितना कम हो वह वस्तु उतनी ही अधिक चमकीली होती है। पृथ्वी पर बैठे हुए प्रेक्षक के लिए मैग्निट्यूड का मतलब है: +6 से अधिक मैग्निट्यूड वाली वस्तुएँ इतनी धुँधली होतीं हैं के बिना दूरबीन के देखी ही नहीं जा सकती। धुँधली-सी दिखने वाली एण्ड्रोमेडा गैलेक्सी का मैग्निट्यूड +3 है। आकाश में रोशन तारे, व्याध तारा, का मैग्निट्यूड -1 है। पूर्णिमा के पूरे चाँद का मैग्निट्यूड -13 है। चढ़े हुए सूरज का मैग्निट्यूड -26.7 है(यानि शुन्य से लगभग 27 कम)। वापस दूरी मापांक समीकरण पर आते है।

उदाहरण के लिए, मान लीजिए एक खगोलविद ने 34 दिनों की अवधि के साथ एक सीफीड सितारा के उज्ज्वलता को मापा है। उस सीफीड तारे का निरपेक्ष कांतिमान -5.65 मैग्निट्यूड है जबकि उसका सापेक्ष कांतिमान +23.0 मैग्निट्यूड दर्ज किया गया है। अब खगोलविज्ञानी इस दूरी मापांक समीकरण का उपयोग कर सकते है।

m – M = 5 log d – 5

यहाँ, m = सापेक्ष कांतिमान, M = निरपेक्ष कांतिमान, d = दूरी पारसेक(pc).
व्यवस्थित करने पर,
d = 10^(m – M + 5)/5 parsecs
सीफीड तारे के आंकड़े रखने पर,
d = 10^(23 – -5.65 + 5)/5 parsecs
d = 10^6.73 parsecs
d = 5.4 × 10^6 parsecs

सीफीड मापन विधि से वैज्ञानिक द्वारा 1 किलो पारसेक से लेकर 50 मेगा पारसेक तक की दूरी का आंकलन किया जाता है। नासा के अनुसार भू-आधारित टेलिस्कोप इस विधि का उपयोग कर 13 मिलियन प्रकाशवर्ष दूर स्थित तारों की दूरी माप रहे है जबकि अंतरिक्ष में स्थापित हब्बल टेलिस्कोप या अन्य बड़े टेलिस्कोप तो 56 मिलियन प्रकाशवर्ष से ज्यादा दूरी तक इस तकनीक का बेहतर उपयोग कर रहे है।

सुपरनोवा मापन(la Supernova Measurement):

सुपरनोवा मापन(la Supernova Measurement): खगोलशास्त्र में सुपरनोवा किसी तारे के भयंकर विस्फोट को कहते हैं। सुपरनोवा नोवा से अधिक बड़ा धमाका होता है और इस से निकलता प्रकाश और विकिरण इतना ज़ोरदार होता है के कुछ समय के लिए अपने आगे पूरी आकाशगंगा को भी धुंधला कर देता है लेकिन फिर धीरे-धीरे ख़ुद धुंधला हो जाता है। जब तक सुपरनोवा अपनी चरमसीमा पर होता है, वह कभी-कभी कुछ ही हफ़्तों या महीनो में इतनी उर्जा प्रसारित कर सकता है जितनी की हमारा सूरज अपने अरबों साल के जीवनकाल में करेगा।

सुपरनोवा तारें खगोलविज्ञानियों के लिए बड़े काम की चीज है क्योंकि सुपरनोवा तारा विस्फोट से गैसों के बादल अंतरिक्ष में प्रसारित हो जाते हैं। ये गैसें नये तारों के निर्माण हेतु कच्चे पदार्थ(raw materials) प्रदान करते है साथ ही सुपरनोवा तारें खगोलीय दूरी मापने के काम भी आते है।

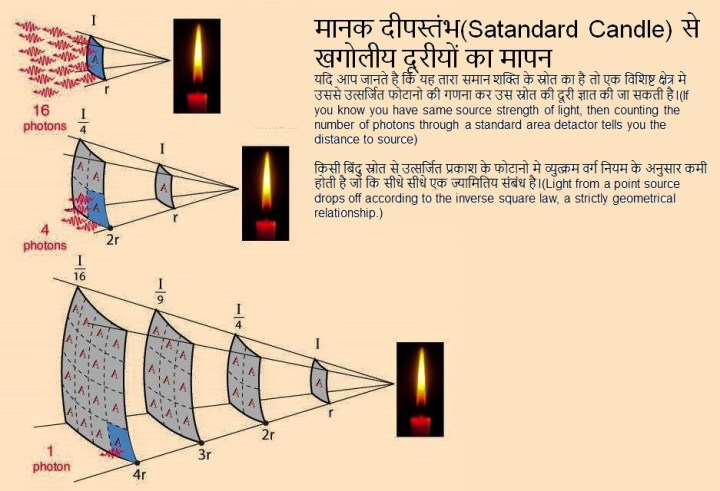
जब खगोलीय दूरी बहुत ज्यादा होती है तब लंबन विधि(parallax method) या सिफीड परिवर्तन(Cepheid variables) विधियों से दूरी का प्रत्यक्ष आंकलन करना संभव नही होता। खगोलविज्ञानियों के अनुसार जब 1 बिलियन प्रकाशवर्ष से ज्यादा की दूरी हो तो लंबन या सिफीड परिवर्तन विधियां सीधे तौर पर काम मे नही आती ऐसी स्थितियों में वैज्ञानिक सुपरनोवा तारें के माध्यम से खगोलीय दूरी का आंकलन करते है। खगोलविदों तब मानक दीपस्तंभ(standard candles) मानी जानेवाली सुपरनोवा को उपयोग में लाने वाली तरीकों की ओर अपना ध्यान केंद्रित करती है। इस तकनीक में वैज्ञानिक सर्वप्रथम किसी ऐसे पिंड को चुनते है जिसका निरपेक्ष कांतिमान उन्हें ज्ञात हो फिर तुलनात्मक रूप से देखा जाता है की वह पिंड अपने सापेक्ष किसी सुपरनोवा विस्फ़ोट से कितनी तीव्रता का प्रकाश ग्रहण करता है। इसी तुलनात्मक आधार पर किसी मापे जानेवाले पिंड(जिस खगोलीय पिंड के दूरी का मापन करना हो) का निरपेक्ष/सापेक्ष कांतिमान का आंकलन किया जाता है। अब प्रकाश तीव्रता का व्युत्क्रम वर्ग नियम(inverse square law for light intensity) का उपयोग खगोलीय दूरी मापन के काम मे लाया जाता है। कुछ विशेष प्रकार के सुपरनोवा की अनूठी विशेषताओं और विशाल चमक खगोलीय दूरी निर्धारित करने की अनुमति हमें देते रहे है।

खगोलविज्ञानी सुपरनोवा के दूरी का आंकलन ज्यादातर सिफीड परिवर्तन के आधार पर करते है क्योंकि उसकी चमक बढ़ जाती है और फिर बाद में मंद हो जाती है। कुछ सुपरनोवा ऐसे होते है जो नियमित समय अंतराल में अपनी चमक को तेज और मंद करते है ऐसे सुपरनोवा को la प्रकार(type Ia) का सुपरनोवा कहा जाता है। खगोलविज्ञानी la प्रकार के सुपरनोवा की अधिकतम चमक(1/distance^2 rule) को ज्ञात करते है जो एक प्रकाशवर्ष की दूरी तक सभी तारों के लिए समान मानी जाती है। इस प्रकार के la सुपरनोवा हमारे मानक मोमबत्तियां(standard candles) मानी जाती है।

यदि दूर की आकाशगंगा की दूरी की मापन करना हो तो सबसे पहले वैज्ञानिक एक प्रकार के la सुपरनोवा का पता लगाते है और फिर उसकी चमक को नियमित रूप से मापा जाता है। इस प्राप्त परिणाम की तुलना ऐसे सभी सुपरनोवों द्वारा प्राप्त ज्ञात अधिकतम उज्ज्वलता के साथ किया जाता है। इस विधि से आकाशगंगाओं की दूरी निर्धारित करने में मदद मिलती है। नासा के वैज्ञानिकों के अनुसार, चूंकि सुपरनोवा बेहद उज्ज्वल होता है इसलिए यह विधि बहुत बड़ी दूरियों के लिए उपयोगी है। फ़िलहाल लगभग एक अरब प्रकाशवर्ष से लेकर 6 अरब प्रकाशवर्ष तक की दूरियों के लिए यह विधि ज्यादा उपयोग में लायी जा रही है।

लाल विचलन और हबल सिद्धान्त द्वारा मापन(Redshift and Hubble’s Law Measurement)

लाल विचलन और हबल सिद्धान्त द्वारा मापन(Redshift and Hubble’s Law Measurement): अमेरिकी खगोलविज्ञानी एडविन पॉवेल हबल(Edwin Powell Hubble) ने सन 1929 में अपने खगोलीय प्रेक्षण से यह खोज निकाला की कोई आकाशगंगा पृथ्वी से जितनी दूर होती है वह उतनी ही तेजी से पृथ्वी से और दूर होती जाती है। उन्होंने खगोलीय प्रेक्षण के दौरान पाया की आकाशगंगा जितनी दूर हो उन आकाशगंगाओं से आने वाले प्रकाश का डॉप्लर प्रभाव उतना ही अधिक होता है, सरल शब्दों में कहे तो उनके प्रकाश में लालिमा अधिक प्रतीत होती है क्योंकि उनसें उत्सर्जित प्रकाश वर्णक्रम में लाल रंग की ओर विचलित हो रहा है। इसे हबल सिद्धांत कहा जाता है और इसका सीधा अर्थ यह निकला की हमारा ब्रह्माण्ड निरंतर फैल रहा है। यह सिद्धांत खगोलशास्त्र मे आकाशीय पिंडों की गति और दूरी को मापने के लिये उपयोग मे लाया जाता है। इस विधि से खगोलीय दूरी मापने से पहले आपको डाप्लर प्रभाव और लाल विचलन को भलीभांति समझना होगा।

डाप्लर प्रभाव(Doppler effect)

डाप्लर प्रभाव(Doppler effect): यह किसी तरंग की तरंगदैधर्य(wavelength) और आवृत्ती(frequency) मे आया वह परिवर्तन है जिसे उस तरंग के श्रोत के पास आते या दूर जाते हुये निरीक्षक द्वारा महसूस किया जाता है। यह प्रभाव आप किसी अपने निकट पहुंचते वाहन की ध्वनी और दूर जाते वाहन की ध्वनी मे आ रहे परिवर्तनो से महसूस कर सकते है। इसे वैज्ञानिक रूप से देंखे तो होता यह है कि आप से दूर जाते वाहन की ध्वनी तरंगो(Sound waves) का तरंगदैधर्य बढ जाती है, और पास आते वाहन की ध्वनी तरंगो का तरंगदैधर्य कम हो जाती है। दूसरे शब्दो मे जब तरंगदैधर्य बढ जाती है तब आवृत्ती कम हो जाती है और जब तरंगदैधर्य कम हो जाती है आवृत्ती बढ जाती है।

लाल विचलन (Red Shift):

लाल विचलन (Red Shift): यह वह प्रक्रिया जिसमे किसी पिंड से उत्सर्जीत प्रकाश वर्णक्रम मे लाल रंग की ओर विचलीत होता है। वैज्ञानिक तौर से यह उत्सर्जीत प्रकाश किरण की तुलना मे निरिक्षित प्रकाश किरण के तरंगदैधर्य मे हुयी बढोत्तरी या उसकी आवृती मे कमी है। दूसरे शब्दो मे प्रकाश श्रोत से प्रकाश के पहुंचने तक प्रकाश किरणो के तरंगदैधर्य मे हुयी बढोत्तरी या उसकी आवृती मे कमी होती है।

प्रकाश किरणों मे लाल रंग की प्रकाश किरणों का तरंगदैधर्य सबसे ज्यादा होता है, इसलिये किसी भी रंग की किरण का वर्णक्रम मे लाल रंग की ओर विचलन ‘लाल विचलन’ कहलाता है। यह प्रक्रिया अप्रकाशिय किरणों (गामा किरणें, X किरणें, पराबैगनी किरणें) के लिये भी लागु होती है और इसी नाम से जानी जाती है। वैसी किरणें जिनका तरंगदैधर्य लाल रंग की किरणों से भी ज्यादा होता है (अवरक्त किरणें(infrared), सूक्ष्म तरंगें(Microwave), रेडीयो तरंगें) यह विचलन लाल रंग से दूर होता है।

सामान्यतः लाल विचलन उस समय होता है जब प्रकाश श्रोत प्रकाश निरिक्षक से दूर जाता है, बिलकुल ध्वनी तरंगो के डाप्लर सिद्धांत की तरह !

खगोलविज्ञानी दूर की आकाशगंगाओं के लाल विचलन को सटीकता से मापने के लिए स्पेक्ट्रोस्कोपी(spectroscopy) का उपयोग करते है। प्रकाश किरणें जब किसी प्रिज्म पर पड़ती है तब वह सात रंगों(ROYGBIV) में विभक्त हो जाती है इसे ही स्पेक्ट्रम या स्पेक्ट्रा(spectrum) कहते है। खगोलविज्ञानी सितारों या आकाशगंगाओं से प्राप्त स्पेक्ट्रम को सामान्य स्पेक्ट्रम से उसकी तुलना करते है। ये उत्सर्जित वर्णक्रम किसी रासायनिक तत्व या रासायनिक यौगिक से उत्पन्न होने वाले विद्युतचुंबकीय विकिरण होते है जो हमें अरबों प्रकाशवर्ष दूर स्थित तारों व ग्रहों की रसायनिक रचना समझने में भी मददगार होते है। वैज्ञानिक तुलनात्मक रूप से देखते है की अवशोषण या उत्सर्जन वर्णक्रम लाइनें कितनी स्थानांतरित(shift) हो जाती है इससे पता चलता है की वह पिंड हमसे कितना दूर है।

बहुत-बहुत दूर स्थित पिंडो ख़ासकर क्वासर(quasars) जैसे पिंड के वर्णक्रम स्पेक्ट्रोस्कोपी के माध्यम से भी बहुत धुँधले दिखाई देते है क्योंकि इनका लाल विचलन बहुत ज्यादा होता है। ऐसी स्थितियों में वैज्ञानिक फोटोमेट्रिक रेडशिफ्ट(photometric redshifts) से लाल विचलन का पता लगाते है। स्पेक्ट्रोस्कोपी से प्राप्त स्पेक्ट्रम यदि ज्यादा धुंधला हो तो विभिन्न फिल्टर के माध्यम से भी स्पेक्ट्रम का अध्ययन किया जाता है। लाल विचलन को लाल विचलन पैरामीटर z(redshift parameter z) से सूचित किया जाता है।

z = (λobserved – λemitted)/λemitted.

यहां, λobserved = स्पेक्ट्रम लाइन में देखा गया तरंगदैर्ध्य
λemitted = सामान्य अवस्था मे स्रोत का तरंगदैर्ध्य

यहाँ आप ध्यान दे, z आपको वर्षों की संख्या बताता है जो वस्तु से प्रकाश आपके पास पहुँचने में लगा समय है। यह पृथ्वी से उस वस्तु की वास्तविक दूरी नहीं है क्योंकि ब्रह्मांड विस्तार कर रहा है इसलिए वस्तु, z संख्या के मुकाबले पृथ्वी से बहुत दूर होती है।

हमसब जानते है, कोई आकाशगंगा पृथ्वी से जितनी दूर होती है वह उतनी ही तेजी से पृथ्वी से और दूर होती जा रही है और इसे हबल स्थिरांक परिभाषित करता है। जिसे गणितीय रूप से इस समीकरण से प्रदर्शित किया जाता है।
V = H × D ….(1)
V = HoD ….(2)
यहां V= वेग, H/Ho = हबल स्थिरांक, D = दूरी

हालांकि हबल स्थिरांक का सटीक मान अभी भी कुछ अनिश्चित है लेकिन आम तौर पर दूरी के प्रत्येक मेगापारसेक के लिए लगभग 65~71 किलोमीटर प्रति सेकेंड माना जाता है। एक मेगापारसेक(1Mpc) का मतलब 3×10^6 प्रकाशवर्ष होता है। इसका मतलब यह है की एक आकाशगंगा यदि हमसे 1 मेगापारसेक दूर हो तो 65 Km/s की रफ्तार से दूर होता जा रहा है जबकि कोई आकाशगंगा यदि 100 मेगापारसेक की दूरी पर हो तो वह इससे 100 गुना तेज गति से दूर होती जाएगी। हबल स्थिरांक ब्रह्मांड का विस्तार करने वाली दर को दर्शाता है।

खगोलविज्ञानियों द्वारा स्पेक्ट्रम के इस बदलाव से उसकी लाल विचलन पैरामीटर z निर्धारित करते है। इस लाल विचलन z के आधार पर यह पता चलता है की प्रकाश को स्रोत/आकाशगंगा से पृथ्वी पर आने में कितना समय लगा। इतनी दूरी पर वहाँ विस्तार की दर को हबल समीकरण से ज्ञात किया जाता है और फिर पृथ्वी से उस पिंड की दूरी निर्धारित की जाती है। यहां आप यह भी ध्यान दें की दूरी निर्धारित करने की यह विधि अवलोकन(स्पेक्ट्रम में बदलाव) और एक सिद्धांत(हबल सिद्धान्त) पर आधारित है। यदि हबल सिद्धांत सही नहीं है, तो इस तरह से दूरी का आंकलन करना गलत हो सकता है लेकिन अधिकांश खगोलविदों का मानना है की हबल सिद्धांत ब्रह्माण्ड में दूरी की एक बड़ी रेंज के लिए बिल्कुल सही हैं। इस खगोलीय विधि से 1 अरब प्रकाशवर्ष से लेकर 30 अरब प्रकाशवर्ष तक की दूरी का आंकलन किया जा सकता है।

 

स्रोत:

• NASA.
• Las Cumbres Observatory.
• National Science Foundation.
• Wikipedia.

लेखिका परिचय

पलल्वी  कुमारी, बी एस सी प्रथम वर्ष की छात्रा है। वर्तमान  मे राम रतन सिंह कालेज मोकामा पटना मे अध्यनरत है।