पांच तरह के सुपरस्ट्रींग सिद्धांत एक दूसरे से भिन्न लगते है लेकिन भिन्न स्ट्रींग द्वैतवाद के प्रकाश मे मे वे एक ही सिद्धांत के भिन्न पहलू के रूप मे आते है। दो सिद्धांत जब एक जैसी भौतिक प्रक्रिया की व्याख्या करते है तब उन्हे द्वैत(dual) सिद्धांत कहते है।
प्रथम प्रकार का द्वैतवाद T-द्वैतवाद(T -Duality) है। यह द्वैतवाद एक R त्रिज्या वाले वृत्त पर संकुचित सिद्धांत(compatified) को 1/R त्रिज्या वाले वृत्त पर संकुचित सिद्धांत से जोड़ता है। अर्थात एक सिद्धांत मे आयाम एक छोटे वृत्त पर लिपटा हुआ है लेकिन दूसरे सिद्धांत मे आयाम एक विशाल वृत्त पर लिपटा हुआ है(संकुचन नाम मात्र का हुआ है) लेकिन दोनो सिद्धांत एक जैसी भौतिक प्रक्रियाओं की व्याख्या कर रहे हैं। प्रकार IIA तथा IIB सुपरस्ट्रींग सिद्धांत T-द्वैतवाद द्वारा एक दूसरे से संबधित है, वहीं पर SO(32) हेटेरोटीक तथा E(8) x E(8) हेटेरोटीक सिद्धांत भी T-द्वैतवाद द्वारा एक दूसरे से संबधित हैं।
दूसरे तरह के द्वैतवाद S-द्वैतवाद(S- Duality) मे एक सिद्धांत की मजबूत युग्मन सीमा(Strong Coupling Limit) को दूसरे सिद्धांत की कमजोर युग्मन सीमा(Weak Coupling Limit) से जोड़ा जाता है। उदाहरण के लिये SO(32) हेटेरोटीक तथा प्रकार I के स्ट्रींग सिद्धांत 10 आयामो मे स्ट्रींग S-द्वैतवाद से जुड़े है। इसका अर्थ है कि SO(32) हेटेरोटीक स्ट्रींग की मजबूत युग्मन सीमा प्रकार 1 की कमजोर युग्मन सीमा के तुल्य है, इसके अतिरिक्त इसका विपरीत भी सत्य है। मजबूत और कमजोर युग्मन सीमा के मध्य द्वैतवाद की खोज का प्रमाण पाने का एक उपाय हर चित्र मे प्रकाश वर्णक्रम अवस्थाओं की तुलना करना है और देखना है कि वे एक जैसी है या नही। उदाहरण के लिये प्रकार I स्ट्रींग सिद्धांत की D-स्ट्रींग अवस्था कमजोर युग्मन मे भारी होती है लेकिन मजबूत युग्मन मे हल्की होती है। यह D-स्ट्रींग SO(32) हेटेरोटीक सिद्धांत के विश्वप्रतल(worldsheet) पर समान प्रकाश अवस्था रखेंगी, इसलिये प्रकार I के सिद्धांत मे यह D स्ट्रींग मजबूत युग्मन मे अत्यंत हल्की होगी, इस तरह से कमजोर युग्मित हेटेरोटीक स्ट्रींग(weakly coupled heterotic string) व्याख्या सामने आती है। 10 आयामो मे S-द्वैतवाद मे स्वयं से संबधित सिद्धांत IIB है जोकि एक IIB स्ट्रींग की मजबूत युग्मन सीमा को S-द्वैतवाद से दूसरी IIB स्ट्रींग की कमजोर युग्मन सीमा से जोड़ता है। IIB सिद्धांत मे एक D-स्ट्रींग भी है जो मजबूत युग्मन पर हल्की होती है लेकिन यह D स्ट्रींग किसी अन्य मूलभूत IIB प्रकार की स्ट्रींग जैसे लगती है।
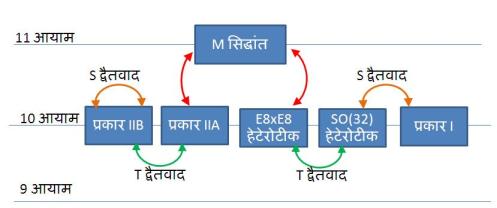
1997 मे गणितज्ञ भौतिकशास्त्री एडवर्ड वीट्टन ने प्रस्तावित किया कि प्रकार IIA तथा E8xE8 एक नये आयामो वाले सिद्धांत “M सिद्धांत” द्वारा एक दूसरे से संबधित है। इस खोज से सभी पांच तरह के स्ट्रींग सिद्धांतो के मध्य की गुम कड़ी(स्ट्रींग द्वैतवाद) का पता चला। इन स्ट्रींग सिद्धांतों के मध्य के द्वैतवाद के कारण ये सभी सिद्धांत एक ही मूल सिद्धांत की भिन्न भिन्न व्याख्या करते है। हर सिद्धांत की अपनी सीमा और व्याख्या है, एक सिद्धांत की सीमा के बाहर दूसरा सिद्धांत प्रभावी हो जाता है लेकिन मूल सिद्धांत एक ही रहता है।
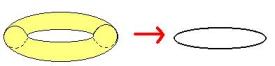
कम ऊर्जा पर M सिद्धांत की व्याख्या 11 आयामो वाले महागुरुत्व सिद्धांत(Supergravity) से की जा सकती है। इस सिद्धांत मे एक मेमब्रेन(membrane – सतह) तथा 5-ब्रेन है लेकिन कोई स्ट्रींग नही है। लेकिन स्ट्रींग सिद्धांत मे स्ट्रींग कैसे नही है ? हम 11 आयामो वाले M सिद्धांत को 10 आयाम वाले सिद्धांत के लिये एक छोटे वृत्त पर संकुचित कर देते है। यदि हम किसी टोरस(torus)* की सतह को किसी वृत्त के रूप मे लपेट दे अर्थात एक आयाम कम कर दे, तब उसकी सतह एक बंद स्ट्रींग के रूप मे आ जायेगी। अर्थात 11 आयामो वाले स्ट्रींग सिद्धांत को 10 आयामो मे संकुचित करने पर प्रकार IIA स्ट्रींग दिखायी देती है।
अब हम कैसे जानते है कि एक वृत्त पर M-सिद्धांत प्रकार IIA की सुपरस्ट्रींग देता है, वह IIB या हेटेरोटीक सुपरस्ट्रींग नही देता है ?
इसका उत्तर 11 आयामी महागुरुत्व के एक वृत्त पर संकुचन से उत्पन्न द्रव्यमान रहित बल-क्षेत्र(massless gauge fields) के ध्यानपूर्वक अध्ययन से मिलता है। दूसरी आसान जांच है कि हम M-सिद्धांत की उत्पत्ति प्रकार IIA की D-ब्रेन अवस्थाओं मे देख सकते है, जोकि केवल प्रकार IIA मे हैं। इस स्थिती को निचे दी गयी सारणी मे देखा जा सकता है।
| एक वृत्त पर M सिद्धांत | 10 आयामो मे IIA सिद्धांत |
|---|---|
| एक वृत्त पर लपेटा मेमब्रेन | प्रकार IIA सुपरस्ट्रींग |
| मेमब्रेन का शून्य आकार मे संकुचन | D0-ब्रेन |
| खुला हुआ मेमब्रेन | D2-ब्रेन |
| वृत्त पर लिपटा हुआ 5-ब्रेन | D4-ब्रेन |
| खुला हुआ 5-ब्रेन | NS 5-ब्रेन |
इस सारणी मे D6 तथा D8-ब्रेन को छोड़ दिया गया है। D6 ब्रेन को “कालुजा केलिन एकध्रुव -Kaluza Klein Monopole” के जैसा माना जा सकता है जो कि 11 आयामी महागुरुत्व के एक वृत्त पर संकुचन का एक विशेष प्रकार का हल है। D8 ब्रेन की M सिद्धांत मे अभी तक कोई व्याख्या नही है। यह वर्तमान शोधो का विषय है।
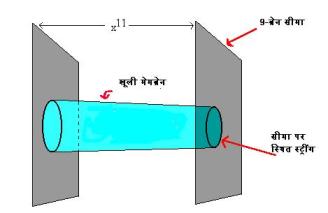
यदि हम M सिद्धांत को एक छोटे रेखाखंड पर संकुचित करे तब भी हमे एक स्पष्ट सिद्धांत मिलता है। इसके लिये 11 आयामो मे से एक आयाम की लंबाई सीमित होती है। इस रेखाखंड के अंतबिंदु अन्य 9 आयामो की सीमायें निर्धारण करते है। एक खूली मेमब्रेन(सतह) इस सीमाओं पर समाप्त हो सकती है। किसी सीमा और सतह का अंतःप्रतिच्छेदन एक स्ट्रींग होती है जिससे हर सीमा के 9+1 आयामो वाले विश्व मे मेमब्रेन के अंतबिंदु से प्राप्त स्ट्रींग हो सकती है। इस सब से यही सिद्ध होता है कि महागुरुत्व सिद्धांत की असंगतियों के निराकरण के लिये हर सीमा पर एक E8 बल समूह चाहीये। इसलिये हम इन सीमाओं के मध्य अंतराल को लघु मान कर चलते है जिससे हमे एक 10 आयामी सिद्धांत जिसमे स्ट्रींग तथा E8 x E8 बल क्षेत्र समूह वाला सिद्धांत प्राप्त होता है। इसे E8 x E8 हेटेरोटीक स्ट्रींग कहते है।
इस तरह से इस नये 11 आयामी स्ट्रींग सिद्धांत तथा उनके अन्य स्ट्रींग सिद्धांत के साथ वाले द्वैतवाद से हमारे पास एक मूलभूत सिद्धांत है जो सभी कणो और बलो की व्याख्या करता है। इसे ही M-सिद्धांत कहते है। सभी पांच सुपरस्ट्रींग सिद्धांत तथा 11-D महागुरुत्व इसकी सीमायें है।
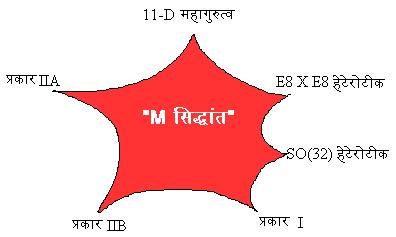
M सिद्धांत अभी संपूर्ण नही है, इस पर अध्ययन जारी है।
अगले भागो मे स्ट्रींग सिद्धांत और श्याम वीवर और स्ट्रींग सिद्धांत की समालोचना
=======================================================================
*टोरस(Torus) : डोनट(Donut) या सांभर-वड़े के वड़ा की आकृती वाला पिंड।


Aur jankaari chaiye quantem physics k baare me. Plz jarur de jaankari.
पसंद करेंपसंद करें
बेहतरीन ज्ञान का भण्डार है यहाँ
धन्यवाद
पसंद करेंपसंद करें
Aabhaar.
पसंद करेंपसंद करें
कठिन लगता है हिन्दी के तकनीकी शब्दों को समझना। शायद तकनीकी विषयों में मेरी हिन्दी पोलियोग्रस्त है। उसे बहुत अधिक फिजियोथेरेपी की जरूरत है! 😦
पसंद करेंपसंद करें
subh prabhatam bhai sahab! Aaj subah subah aapki ye post padhkar man prasanna ho gaya!
Vishwash keejiye, kal hum yahi sonch rahe the ki aapki agli post kab aayegi. Aur subha email check kiya to apki post dekhkar man prasanna ho gaya!
Dhanyawaad
पसंद करेंपसंद करें